引言

在前兩篇的內容，我們看過了 Naive Bayes（用機率來猜分類），還有 Decision Tree & Random Forest（用問問題來做決策）。
今天我們要來看看另一個思路，就是直接畫一條線，把不同類別分開！

圖片來源：https://www.sohu.com/a/386182911_100271825

大家看到上面這張圖會有共鳴嗎XDD 小時候會在桌子上會畫一條「楚河漢界」的線，線的左邊是我的東西，右邊是你的東西，誰都不可以越界！！像這樣用一條線把不同區域劃分清楚的方式，其實就和 「線性分類」 的概念很像～～

所謂的線性分類，就是用一條線 aka. 決策邊界（Decision Boundary） 把不同的類別分開。而我們要思考的關鍵問題就是：「這條線該怎麼畫才最好？」

今天要介紹的是線性分類的經典方法：Logistic Regression。我們會先了解它的計算原理，最後再帶一段程式實作～～

Logistic Regression 羅吉斯迴歸

Logistic Regression 的名字裡雖然有「迴歸」，但它其實是一個分類模型。用來算一個東西屬於某個類別的機率。
它的計算方式主要有三個核心概念：

1. 線性組合

這個算法可以想像成某一門課要算總成績，會把整學期的考試算加權：

• 期中考佔 40%，考 80 分 → 加權後 32 分
• 期末考佔 60%，考 70 分 → 加權後 42 分
• 總分 = 32 + 42 = 74 分

這個線性方程式就是把所有的 特徵 x 乘上不同的 權重 w（weight），然後全部加起來會算出一個 分數 z。

• 在 2 維的空間裡是一條直線
• 在 3 維裡是一個平面
• 在更高維度裡就是超平面（hyperplane）

這個「線」或「面」就是 決策邊界（Decision Boundary）。

2. Sigmoid 轉換

透過 Sigmoid 函數，可以把 𝑧 壓縮至 0 和 1 之間。如果 𝑧 很大，輸出會趨近 1，反之則趨近 0。

圖片來源：https://developers.google.com/machine-learning/crash-course/logistic-regression/sigmoid-function?hl=zh-tw

這個結果就能被解讀成「屬於某一類的機率」。例如，現在的任務為「電影評論正負向情緒分類任務」，可以理解為我們要判斷電影評論「是否為正向」：

• 當計算結果為 0.85，就可以解釋為有 85% 的機率屬於正面評論
• 當計算結果為 0.2，就代表只有 20% 的機率屬於正面評論（意即偏向負面評論）

3. 依據機率分類

使用 Sigmoid function 把分數轉成 0~1 的機率後，就可以根據閾值決定分類結果。通常閾值會設在中間 0.5，也就是說大於 0.5 偏向正向；小於 0.5 偏向負向。

程式實作

1. 前置預備（詳細步驟分解可以參考這篇 Naive Bayes）

• 讀取資料：kaggle 的 IMDb 50K Cleaned Movie Reviews
• 資料劃分：訓練集跟測試集切分為 8:2
• 特徵轉換：文字轉為 TF-IDF 向量

import kagglehub
import pandas as pd
import os
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer

# 讀取資料
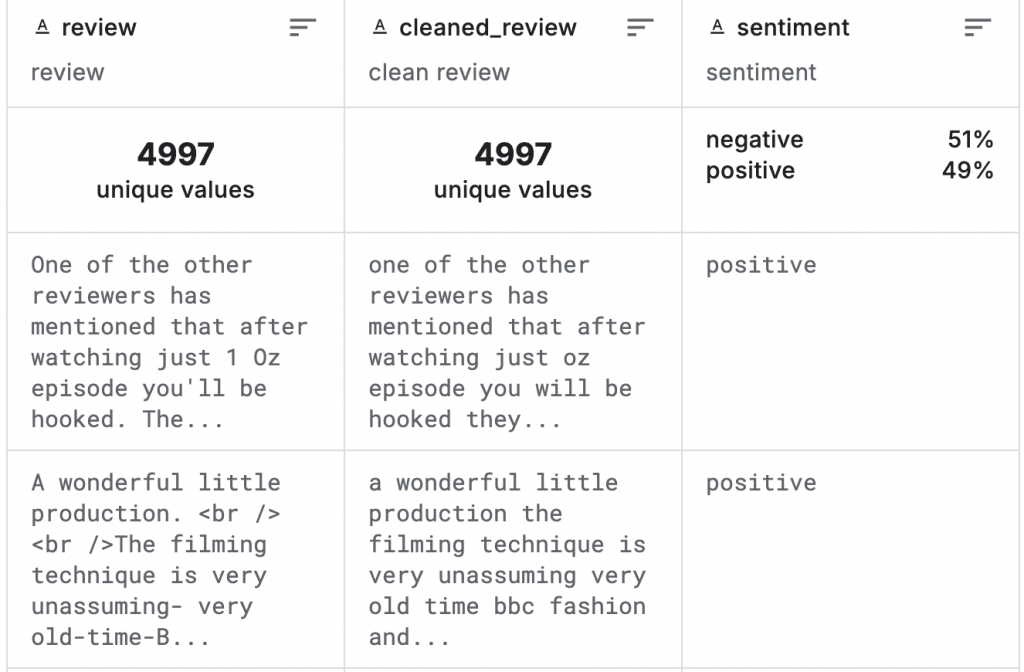
path = kagglehub.dataset_download("ibrahimqasimi/imdb-50k-cleaned-movie-reviews")
csv_path = os.path.join(path, "IMDB_cleaned.csv")  
df = pd.read_csv(csv_path)

# 資料劃分
X = df["cleaned_review"]
y = df["sentiment"]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 特徵轉換
vectorizer = TfidfVectorizer(stop_words="english", max_features=5000)
X_train_vec = vectorizer.fit_transform(X_train)
X_test_vec = vectorizer.transform(X_test)

2. Logistic Regression 模型訓練與評估

from sklearn.linear_model import LogisticRegression

# 建立模型
LR_model = LogisticRegression(max_iter=200, random_state=42)
LR_model.fit(X_train_vec, y_train)
y_pred = LR_model.predict(X_test_vec)

# 評估
print("=== Logistic Regression ===")
print("Accuracy:", accuracy_score(y_test, y_pred))
print("Precision:", precision_score(y_test, y_pred, pos_label="positive"))
print("Recall:", recall_score(y_test, y_pred, pos_label="positive"))
print("F1 Score:", f1_score(y_test, y_pred, pos_label="positive"))
print("\n分類報告:\n", classification_report(y_test, y_pred))

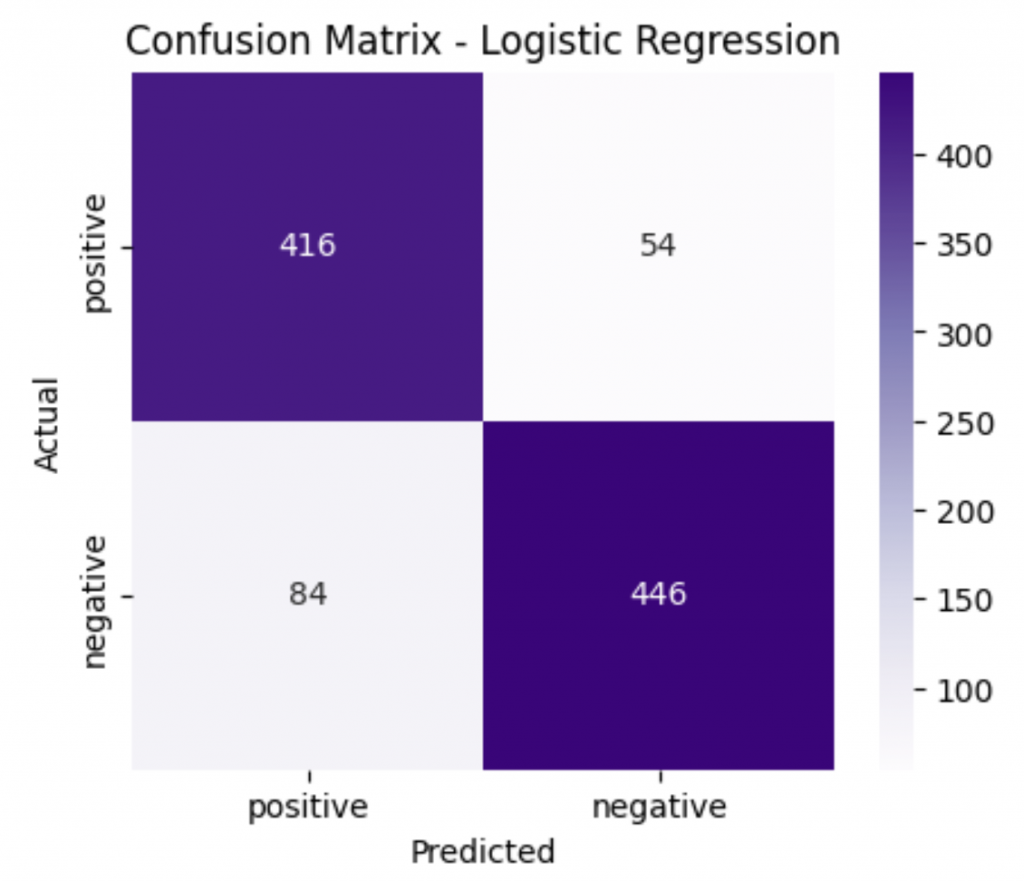
# 混淆矩陣
cm = confusion_matrix(y_test, y_pred, labels=["positive", "negative"])
plt.figure(figsize=(5,4))
sns.heatmap(cm, annot=True, fmt="d", cmap="Purples",
            xticklabels=["positive", "negative"],
            yticklabels=["positive", "negative"])
plt.xlabel("Predicted")
plt.ylabel("Actual")
plt.title("Confusion Matrix - Logistic Regression")
plt.show()

=== Logistic Regression ===
Accuracy: 0.862
Precision: 0.832
Recall: 0.885
F1 Score: 0.858

分類報告:
               precision    recall  f1-score   support

    negative       0.89      0.84      0.87       530
    positive       0.83      0.89      0.86       470

    accuracy                           0.86      1000
   macro avg       0.86      0.86      0.86      1000
weighted avg       0.86      0.86      0.86      1000

結語

Logistic Regression 就是一個 「分數加權平均 + Sigmoid 函數」 的組合。這個方法讓我們能把輸入的數據轉換成一個機率，再依照這個機率來做分類。
它的好處是直觀、解釋性高，不過在面對一些比較複雜的資料分布時，劃出來的那條「決策邊界」可能就不夠精準。

那麼，有沒有辦法找到一條「分界線」，不只可以分開不同類別，還能盡量拉開它們的距離，讓分類更確實呢？
答案就是明天要介紹的 SVM（Support Vector Machine）！！明天見啦～～

References

• [資料分析&機器學習] 第3.3講：線性分類-邏輯斯回歸(Logistic Regression) 介紹